分组汇总

本节将以一个多层分组汇总报表为例，讲述格集的概念和用法。

一个例子

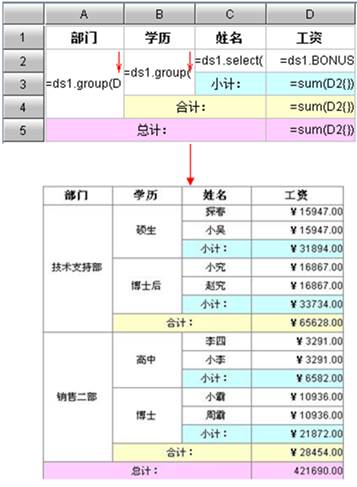
上面的例子是一个多层分组报表，报表按“部门”、“学历”做了分组，如果我们要统计每一组的工资合计该如何做呢？我们来看集算是如何实现的。

D3单元格输入表达式：=sum(D2{})，该单元格随B2单元格的扩展而扩展，因此，该单元格统计的是每一组学历下所有员工的工资之和；

D4单元格输入表达式：=sum(D2{})，该单元格随A2单元格的扩展而扩展，因此，该单元格统计的是每一组部门下所有员工的工资之和；

D5单元格输入表达式：=sum(D2{})，该单元格是总的汇总，不随任何单元格的扩展而扩展，因此该单元格统计的是所有员工的工资之和。

具体用法请参见：格集表示法

格集

在实际应用中，往往需要对一组单元格进行运算，而不是单个单元格。这些单元格有可能是固定格，也有可能是主动扩展、被动复制格，为了能在表达式中描述确定的一组单元格，我们引入格集的概念。

格集可以看为满足某种条件的一组单元格的集合。特别的，单个单元格也可以视为仅含一个单元格的格集。

为了说明格集的概念及其作用，我们看看下面的表格：

 

例12.5.2-1：

扩展前：

扩展后：

填入数据：

如果我们要进行如下统计：①Tom买牛奶的日期；②Tom买毯子的金额；③Jerry在2005-2-1买的商品；④所有买牛奶的金额。

在做这些统计时，涉及到的数据都是发生在一系列格子中的，我们分别来看一下：①c2,c3；②d4,d5；③d9,d11；④d2,d3,d6,d7,d8。

 

Ø  格集表示法包含固定格的格集表示法和扩展格的格集表示法

固定格的格集表示法：

对于固定的单元格，我们可以用list()函数，：（link）操作符来表示，书写规则如下：

list(Cell1, Cell2, Cell3,……Celln)  表示由Cell1, Cell2, Cell3,……Celln组成的格子的集合

[Cellx : Celly] 其中Cellx与Celly均为单元格，该表达式表示以Cellx与Celly为对角点圈起的矩形区域，而且，Cellx在左上角，Celly在右下角。

提示：Link操作符返回的结果是一个格集，可以对其应用集合函数，如count()、sum()、max()、min()等，但是包含link操作符的单元格不允许设为扩展格。

举例：

list(A1,B3,C4) 表示由A1,B3,C4三个单元格组成的集合

sum([A1:B3])  表示对以A1与B3为对角点圈起的矩形区域里的格子求和。

 

扩展格的格集表示法：

对于扩展格的格集表示，我们一般和层次坐标结合起来，由层次坐标来界定一个范围，在这个范围内的所有单元格的集合，其书写规则如下：

Cellx[层次坐标或者位移坐标]{}

说明：从上述书写规则可以看出，格集相当于在层次坐标或者位移坐标的基础上增加了{}，即可表示该层次坐标或者位移坐标界定的范围内的所有单元格。前文已经提到，如果没有{}，而层次坐标界定的范围内的单元格不止一个，那么该层次坐标返回的是该范围内的第一个单元格，有了{}，就返回该范围内单元格的集合。

 

例12.5.2.1-1：

扩展前：

扩展后：

根据上述表格，我们写几个格集并分析其结果由哪些单元格组成。

C2[`0]{}  返回扩展后的c2,c3,c4,c5,c6,c7,c8,c9,c10,c11,c12

C2[A2:2]{}  返回扩展后的c7,c8,c9,c10,c11,c12

D2[A2:1,B2:2]{}  返回扩展后的d4,d5,d6

 

Ø  缺省格集

同样的，为了简化格集的表示，很多时候会有缺省的写法，其缺省的规则和层次坐标、位移坐标完全一样，主要也是为了简化其中的层次坐标、位移坐标的写法，即目标单元格和当前格的主格相同时，层次坐标（位移坐标）中的该主格可以省略，如果所有主格都相同，则层次坐标（位移坐标）可以为空，甚至连中括号都可以省略。

其书写规则为：

Cellx[缺省的层次坐标或者位移坐标]{}

如果层次坐标（位移坐标）完全省略，则缺省的写法为：

Cellx[]{}或Cellx{}

 

例：12.5.2.2-1

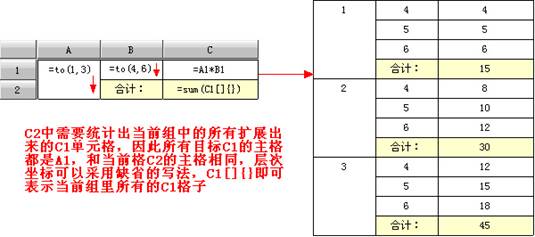
例：12.5.2.2-2